In this blog post, we will get our first taste of what theorycrafting in Genshin Impact looks like, and see some of the math that’s involved.

Calculating ATK, DEF, and Max HP

Before one can do anything theory-related, we must learn how to calculate the ATK, DEF, and Max HP of a character, because these stats affect how much damage a character does against enemies.

For the purpose of these tutorials and demonstrations, we will use three of my own characters and their builds. To see an enlarged version of a character card, just click on the one you want to see.

Conventions

We will use blackboard font letters to denote the total attack, defense, and Max HP of a character, respectively. That is,

\(\newcommand{\A}{\mathbb{A}} \newcommand{\D}{\mathbb{D}} \newcommand{\H}{\mathbb{H}}\) \(\newcommand{\charatk}{\alpha_{\text{char}}} \newcommand{\weapatk}{\alpha_{\text{weap}}} \newcommand{\percentatk}{\wp_{\scriptsize\text{ATK}}} \newcommand{\flatatk}{\alpha_{\text{flat}}}\) \(\newcommand{\chardef}{\delta_{\text{char}}} \newcommand{\percentdef}{\wp_{\scriptsize\text{DEF}}} \newcommand{\flatdef}{\delta_{\text{flat}}}\) \(\newcommand{\charhp}{h_{\text{char}}} \newcommand{\percenthp}{\wp_{\scriptsize\text{HP}}} \newcommand{\flathp}{h_{\text{flat}}}\) \(\begin{align*} \A &= \text{Total Attack} \\ \D &= \text{Total Defense} \\ \H &= \text{Max HP} \end{align*}\)

Furthermore, we will use the following notation: \(\begin{equation*} \begin{aligned}[c] \charatk &= \text{Character's Base ATK} \\ \weapatk &= \text{Weapon's ATK} \\ \percentatk &= \text{ATK Percentage} \\ \flatatk &= \text{Flat ATK} \end{aligned} \qquad\qquad \begin{aligned}[c] \chardef &= \text{Character's Base DEF} \\ \percentdef &= \text{DEF Percentage} \\ \flatdef &= \text{Flat DEF} \end{aligned} \end{equation*}\)

Motivation for Variable Names

I chose $\alpha$ for the ATK-related quantities because $\alpha$ is the Greek letter for “A”, which is the first letter in the word “attack”. Similarly, $\delta$ is the Greek letter for “D”, which is the first letter in the word “defense”.

For the English letter “H”, there is no clear Greek counterpart, so I kept lowercase “h” for all the HP-related quantities.

ATK Formula

Using the aforementioned notation, we have

DEF Formula

We have a similar formula for DEF:

Max HP Formula

The formula for Max HP is analogous to the DEF formula:

Examples

Example ATK Calculation

Let’s calculate Raiden’s ATK using the ATK formula. For ease of reference, I have put her character card below.

Substituting the formula with the numbers, we get

As we can see, our calculated value checks out with the ATK given in the character card.

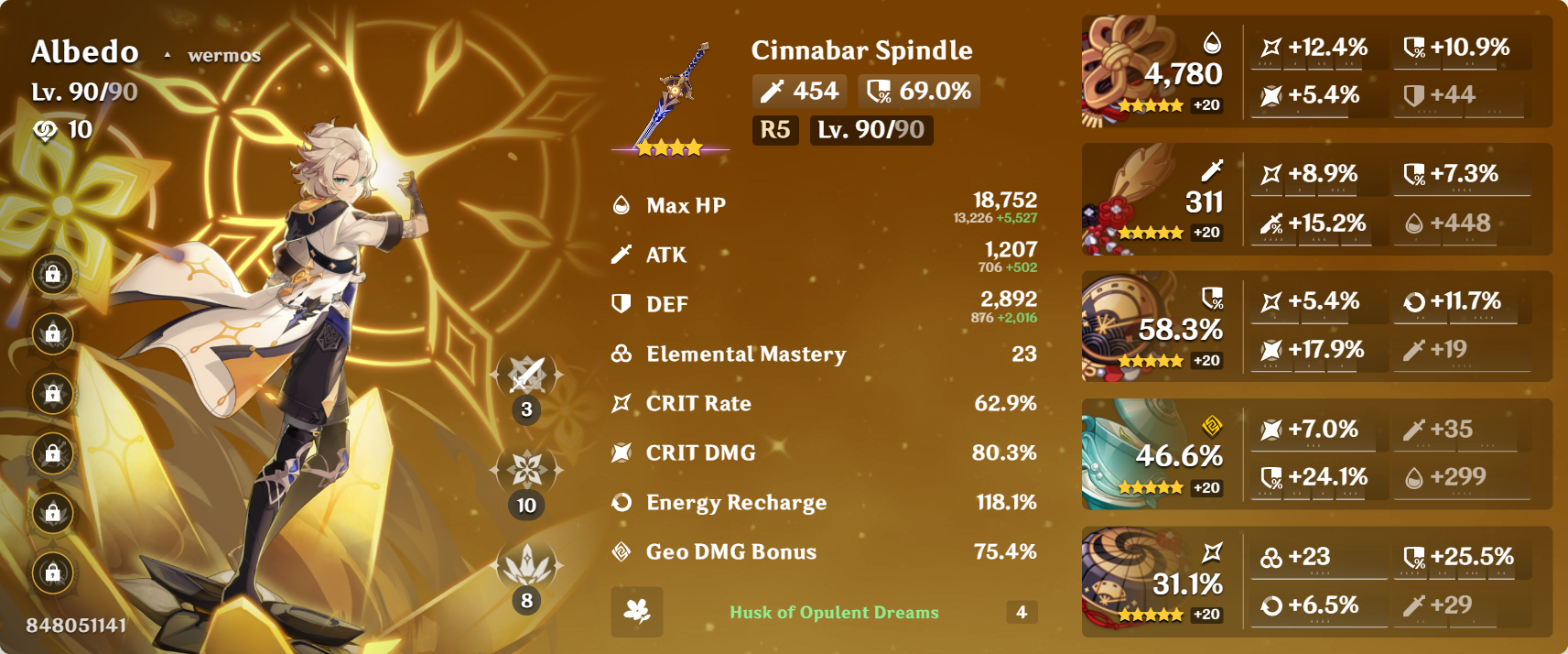
Example DEF Calculation

Now, let’s calculate Albedo’s DEF using the DEF formula. Once again, for ease of reference, I have put his character card below.

Substituting the formula with the numbers, we get

Once again, since our calculated value checks out with the DEF given in the character card, we can be sure that we did the correct calculations.

Albedo’s DEF In Reality

Since I have him on the 4-piece Husk set, he gets an additional 24% DEF bonus when he has all 4 Curiosity stacks. This means that in real-world scenarios, his DEF is \(\begin{align*} \D &= 876\cdot (1 + \underbrace{0.690}_{\mathclap{\substack{\text{Weapon} \\ \text{Substat}}}} + \underbrace{0.583}_{\mathclap{\substack{\text{Sands} \\ \text{Main Stat}}}} + \underbrace{0.678}_{\mathclap{\substack{\text{Artifact} \\ \text{Substats}}}} + \underbrace{0.300}_{\mathclap{\substack{\text{2 pc. Husk} \\ \text{Bonus}}}} + \underbrace{0.240}_{\mathclap{\substack{\text{4 pc. Husk} \\ \text{Bonus}}}}) + \underbrace{44}_{\mathclap{\substack{\text{Flower} \\ \text{Substat}}}} \\ &= 3102.116 \\ &\approx 3102 \end{align*}\)

This is consistent with the numbers which show up in the game.

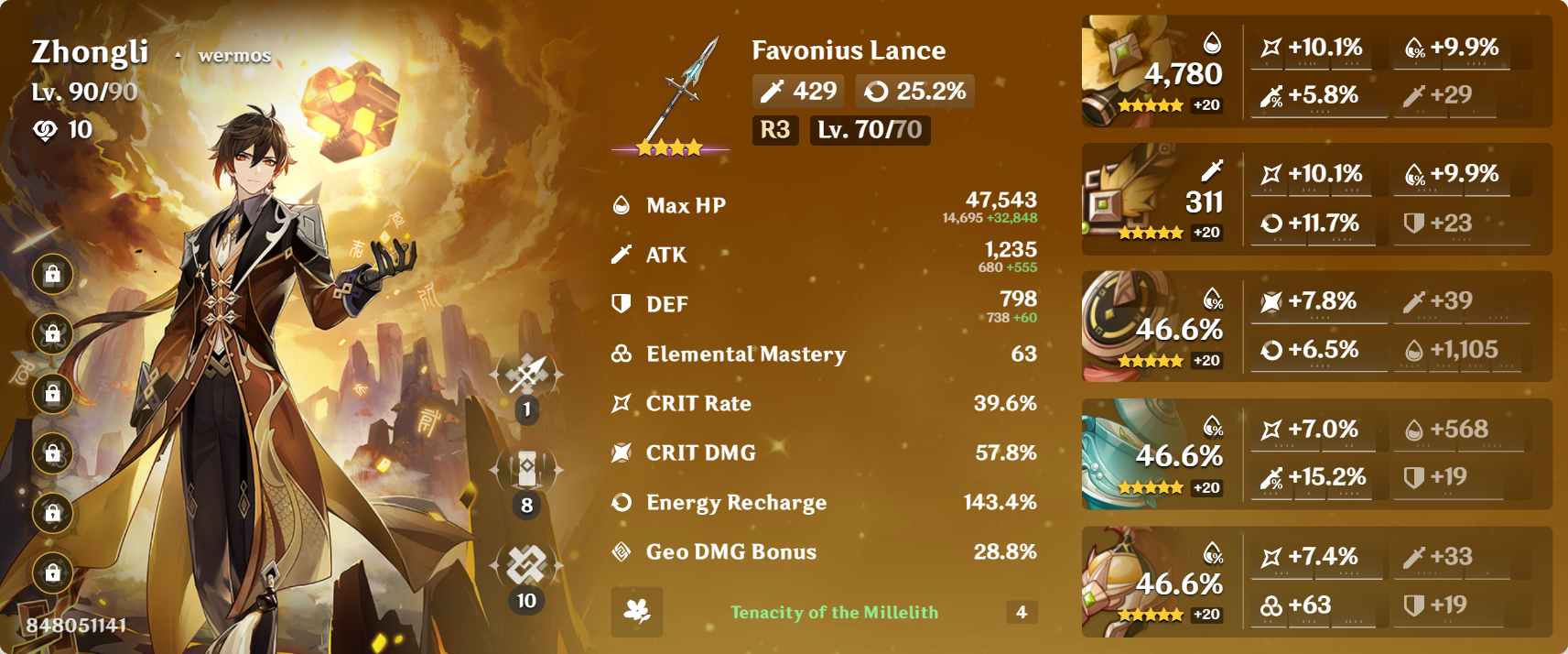
Example Max HP Calculation

Now, let’s calculate Zhongli’s Max HP using the formula. Once again, for ease of reference, I have put his character card below.

Note that the fact that he is using a level 70 weapon is okay because ATK has no bearing on Max HP.

Substituting the formula with the numbers, we get

Observe that our calculated value agrees with the number given in the character card.

Note that we used the value of $0.0991$ instead of the $0.099$ given in the character card. This is because of the way artifact substats are calculated, which we will take a deep-dive into in a future blog post. The extra $0.01\%$ is significant in this case because the value of the quantity we are calculating is in the $40$ thousands, so it does actually make a difference. That being said, the difference it makes amounts to about $3$ HP